
このページでは…
- 中3 1学期の中間テストに向けての対策ができます。
中3の内申は,高校入試にも関係してくるので「頑張ろう!」という気持ちになっている人も多いのではないでしょうか。
そんな人たちのためにこのページでは
- 復習しておくべき例題
- 中3で最初に学ぶ「多項式」のポイント
- ミスしやすい問題の詳しい解説
などが書かれています。
それではさっそく、見ていきましょう。
復習しておくべき問題
中3の1学期の中間テストでは「多項式」がメインで出題される学校が多いと思います。
これは計算の単元です。
この単元までに学習した計算の中で,特に関係性の高いものをピックアップしました。
まずはここにある問題を復習をしましょう。
問:次の式を計算しなさい。【中1文字と式】
① \(2x-3(x+4)\)
- この問題のポイントは「項」です。この式の中には項は2つあります。
1つ目は「\(2x\)」
2つ目は「\(-3(x+4)\)」です。
2つ目の項の,かっこをはずします。
\(=2x-3x-12\)
- かっこを外すときに,「\(-3\)」と「\(+4\)」をかけるのも忘れないようにしましょう。
符号は「マイナス」になります。
\(=-x-12\)
- 同類項をまとめました。
たまに見かけるミスが「\(2x\)と\(-3\)をかけてしまう」というものです。
この式は\(2x\)と\(-3(x+4)\)の2つの項が「+」でつながってできています。
文字と数字がかけられて1つの項を作る場合は文字の前に数字を書く
というルールがあるので、この式の\(2x\)と\(-3\)は何の関係もありません。
どこで式が分かれているのかをわかるようにしておきましょう。
では次の問題です。
② \(-3(x-4)+2\)
- この問題のポイントは「かっこのはずし方」です。
\(=-3x+12+2\)
- かっこを外すときに,「\(-3\)」を「\(x\)」と「\(-4\)」にかけます。
\(=-3x+14\)
- 12+2の部分を計算しました。
この問題で見られるミスとして「\(-3\)を\(+2\)にもかけてしまう」というものがあります。
その結果途中の式が「\(=-3x+12-6\)」のようになってしまったりします。
やはりポイントは「項」で,今回は\(-3(x-4)\)と\(+2\)の2つの項が「+」でつながってできていました。
上の2つの問題に自信がない人は次のファイルを見て確認しておくようにしてください。
中1 文字と式
18 1次式の加法と減法
中2 式の計算
3 多項式の加法と減法
4 多項式の乗法と除法①
中3 多項式に関して必要な復習はこのくらいでOKです。さらに細かい箇所が気になったりわからなかったりしたら,近くの人に聞くようにしましょう。コメント欄で質問も受け付けています。
ではいよいよ,多項式の対策です。
基本の例題をチェックしましょう。
基本例題
問:次の式を計算しなさい。【単項式×多項式】
\(2a(5a-4b)\)
- \(2a\) と \(5a\) をかけます。
- \(2a\) と \(-4b\) をかけます。
\(=10a^2-8ab\)
- まとめられる同類項がないので,これで終わりです。
問:次の式を計算しなさい。【多項式÷単項式】
\(\displaystyle(3x^2+xy)÷\frac{ 1 }{ 2 }x\)
- \(\displaystyle÷\frac{ 1 }{ 2 }x\) の部分の計算の仕方に注意が必要です。
\(\displaystyle÷\frac{ 1 }{ 2 }x\) → \(\displaystyle÷\frac{ x }{ 2 }\) → \(\displaystyle×\frac{ 2 }{ x }\) となります。
\(=\displaystyle3x^2×\frac{ 2 }{ x }+xy×\frac{ 2 }{ x }\)
- \(\displaystyle3x^2×\frac{ 2 }{ x }\) の部分を約分すると
\(x^2\)が\(x\)になって,\(x\)が\(1\)になるので
\(\displaystyle3x×2=6x\) となります。 - \(\displaystyle xy×\frac{ 2 }{ x }\) の部分を約分すると
分母と分子の\(x\)が\(1\)になるので
\(2y\) となります。
\(=6x+2y\)
- \(6x\)と\(2y\)はまとめられません。
※このわり算はミスしてしまう人も多いのでしっかりと練習しておきましょう。
問:次の式を展開しなさい。
① \((x+3)(y+4)\)
- 4つある項をそれぞれすべてかけます。
\(=xy+4x+3y+12\)
- この式の中に同類項は無いので,これで終わりです。
② \((x+3)(x+2)\)
- それぞれかけます。
\(=x^2+2x+3x+6\)
- 同類項があるときは,まとめます。
\(=x^2+5x+6\)
- \(2x\)と\(3x\)をまとめました。
問:次の式を展開しなさい。【乗法公式1】
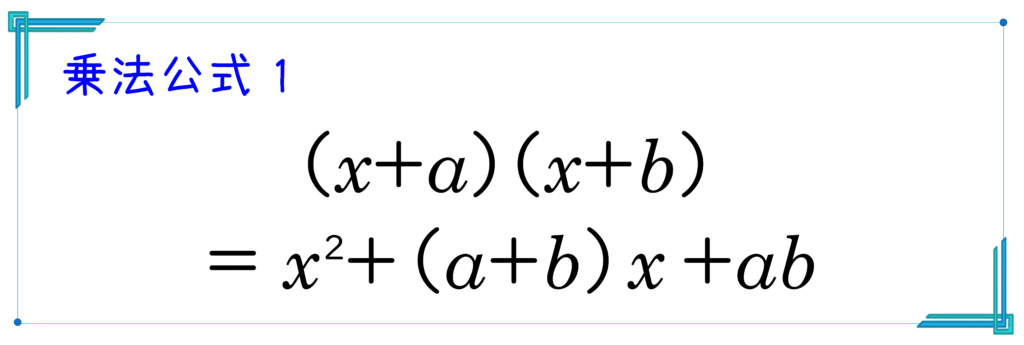
\((x+2)(x+5)\)
- 公式にあてはめます。
\(=x^2+(2+5)x+2×5\)
- 乗法公式1で, \(a=2\),\(b=5\) です。
\(=x^2+7x+10\)
- 慣れてきたら,2行目の式は書かずにすぐにこの答えの行を書くようにしましょう。
問:次の式を展開しなさい。【乗法公式2・3】

① \((x+5)^2\)
- 公式2にあてはめます。
\(=x^2+2×5×x+5^2\)
- 乗法公式2で, \(a=5\)という式です。
\(=x^2+10x+25\)
- これで完成です。
② \((x-4)^2\)
- 公式3にあてはめます。
\(=x^2-2×4×x+(-4)^2\)
- 乗法公式3で, \(a=4\)という式です。
(乗法公式2で, \(a=-4\)であるときだと考えても良いです。)
\(=x^2-8x+16\)
問:次の式を展開しなさい。【乗法公式4】

\((x+4)(x-4)\)
- 公式4にあてはめます。
\(=x^2-4^2\)
- 乗法公式4で, \(a=4\) です。
\(=x^2-16\)
この公式は,できる項の数が「2つ」であるという特徴があります。
いろいろなパターンがある中でこのような「他とちがう部分」に注目して,記憶に残しやすくしましょう。
これらの問題をより詳しく学習したいときは,次のファイルで練習してください。
中3 多項式
1 単項式と多項式の乗法・除法
2 展開
3 乗法公式1
4 乗法公式2・3
5 乗法公式4
次は少し複雑な計算の練習問題です。
問:次の計算をしなさい。
\(3(x-4)^2-(x+6)(x-1)\)
- \(3(x-4)^2\) の部分と \(-(x+6)(x-1)\) の部分それぞれを考えます。
\(=3(x^2-8x+16)-(x^2+5x-6)\)
- \(3(x-4)^2\) の部分は
\((x-4)^2\) を先に計算して,かっこの中に入れます。 - \(-(x+6)(x-1)\) の部分は
\((x+6)(x-1)\) を先に計算して,こちらも同じくかっこの中に入れます。
\(=3x^2-24x+48-x^2-5x+6\)
- それぞれのかっこをはずしました。
\(=2x^2-29x+54\)
- \(3x^2\) と \(-x^2\) をまとめて
\(2x^2\) になりました。 - \(-24x\) と \(-5x\) をまとめて
\(-29x\) になりました。 - \(48\) と \(+6\) をまとめて
\(+54\) になりました。
この問題と似たようなタイプの問題は,次のファイルでさらに練習することができます。
中3 多項式
7 いろいろな展開
学習のポイント
計算の単元が定期テストの範囲だった場合,実は高得点を狙えるチャンスです!
計算は練習すれば確実にできるようになるからです。
どんなに複雑な計算でも,決められたルール通りに進めていけば正解にたどり着きます。
テストに向けて
「ミスなくできるようになるまで練習できているか,できていないか」
その違いが計算の得点の差となって表れてきます。
丁寧に準備をして,良い点数を目指しましょう!