数直線上で正の方向(右側)にあるほど大きく、負の方向(左側)にあるほど小さいといえます。

このページで学ぶこと
- 負の数も含めて考えるとき、「数の大きさ」はどのように考えれば良いか、その方法を学びます。
- 数の大小の表し方を学びます。

これからは、ゼロの左側にも数直線が伸びます。
- 数は数直線上で右側にあるほど「大きい」。左側にあるほど「小さい」と言えます。(右に行くほど大きくなって左に行くほど小さくなると言えます。
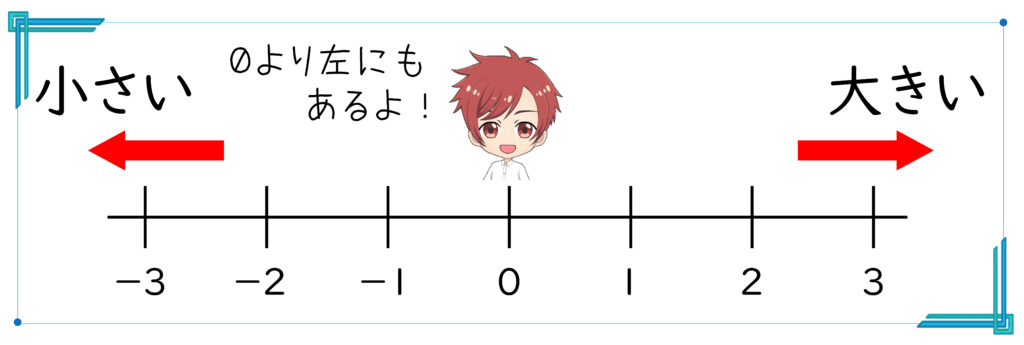
今までは「0」が1番小さい数でしたが、これからは「負の数」も数直線に書くことになります。
2つの数の大小を比べるときは、数直線上でどちらが右にあってどちらが左にあるかを考えましょう。
数直線上で右側にあるほど大きく、左側にあるほど小さい、ということになります。

これからは数の大小を表すときは、不等号を使います。
- 数の大小は不等号を使って表します。
これらの記号(<、>)のことです。
例えば-5と-2では
-5のほうが左側にあるから -5 の方が -2 より小さいと言えます。
このことをこんなふうに表します。
「-5<-2」
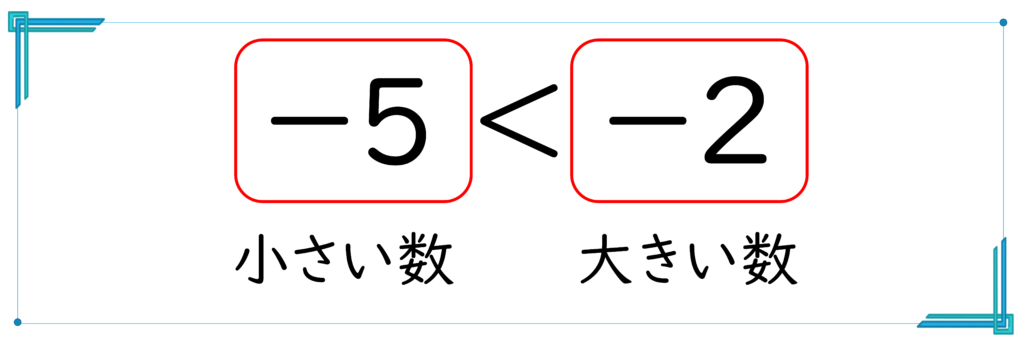
この不等号の閉じている方に小さい数を。開いている方に大きい数を書くようにしてください。
読み方は「-5は-2より小さい」と読んだり「-5小なり-2」と読んだりします
これは「-2>-5」のように表しても良いです。
この場合は「-2大なり-5」と読んだり、「-2は-5より大きい」と読んだりします。
左側に小さい数をかいた方がわかりやすいですね。
なのでふつうはこの書き方「-2>-5」ではなく
左側に小さい数を書く小なりを使う書き方である
「-5<-2」こっちの方を使うようにしましょう。
※ここではこのようにしていますが、学校の授業などで言われた通りにしましょう。
例題でもう少し練習していきます。
例:次の数の大小を,不等号を使って表しなさい。
3 と- 5
これは-5の方が小さいので、 -5<3 となります。
答え -5<3
この順番通りに書きたければ 3>-5 となって、これでも正解にはなります。
-6と-1
これはこの順番通り-6の方が小さいので -6<-1 となります。
答え -6<-1
※数の大小を考えるときは、数直線を頭に思い浮かべると良いです。不等号(<、>)の使い方にも慣れておきましょう。
ちなみに、-0.1と-0.01 では、大きのはどちらになるでしょうか。答えは -0.01 です。